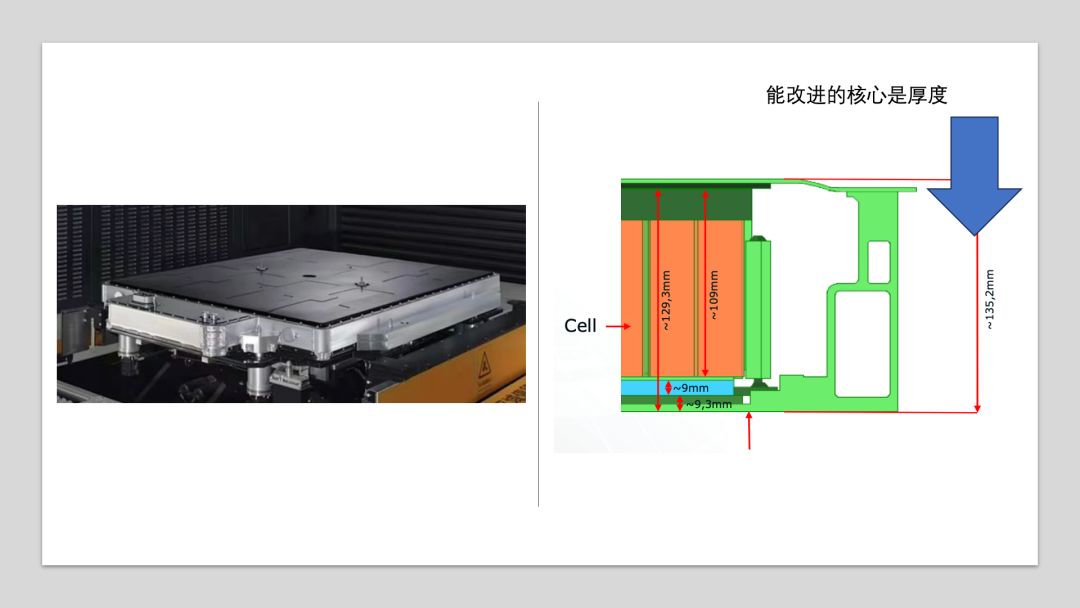
智能电动车
加速汽车智能化转型,打造新质生产力引擎—CICV2024 6月18日在京开幕
第十一届国际智能网联汽车技术年会(CICV 2024)定于2024年6月18-20日在北京·北人亦创国际会展中心举办
新闻资讯
AMD向AI边缘计算开战,单芯片智能为嵌入式系统而生
继第一代VersalITM AI Edge自适应SoC之后,AMD又发布了第二代VersalTM自适应SoC,为边缘计算打开了方便之门。
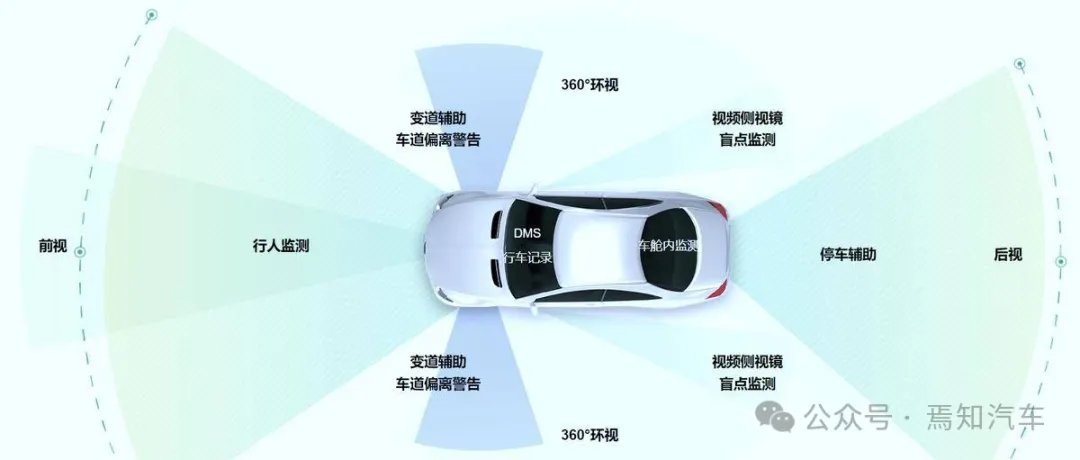
自动驾驶
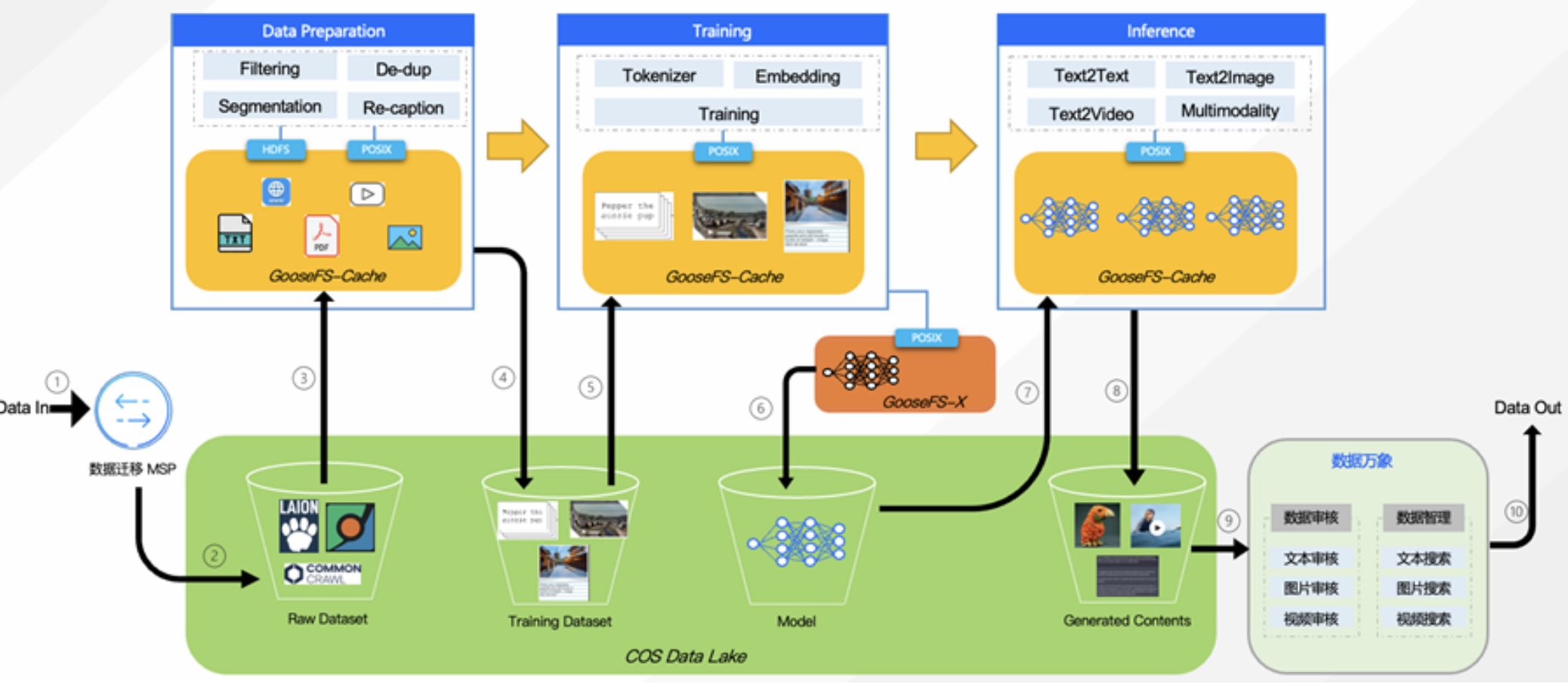
腾讯云COS Data Lake在AIGC和自动驾驶技术领域的最新解决方案
腾讯云COS Data Lake不仅助力AIGC和自动驾驶业务更好地处理和利用大规模数据,也为加速企业数字化转型提供更多可能性。